In this tutorial, we are going to be looking at “merge sort” – an efficient and general-purpose algorithm for handling arrays.
Not only is it one of the best choices for sorting arrays large or small, but knowing how the syntax and logic of the algorithm works will broaden your ability to write better and faster code.
Let’s explore how to use merge sort!
Table of contents
Overview
A merge sort algorithm essentially performs two operations on an array. The first operation is actually sorting the array. The algorithm sorts the entire array by breaking it up into smaller arrays. Let’s take the simplest example of an array of numbers that need to be sorted in ascending order. A merge sort algorithm would take the array and split it into a few smaller arrays until each element belongs to a brand new array. The array elements would then be compared to elements in adjacent arrays. If an element is larger than its adjacent element, then that element is placed after its adjacent element. If the element is smaller, then that element is placed before its adjacent element.
This is how the algorithm sorts elements. However, notice that we still have a single array for each element. We want one array with all elements in order. Thus the algorithm performs the second operation. This operation is merging the sorted subarrays with a merge algorithm. As each single element is compared with its adjacent element, it is stored in a new whole array. This process is repeated until we arrive at one single final array. Here is a diagram that covers the steps the algorithm takes:
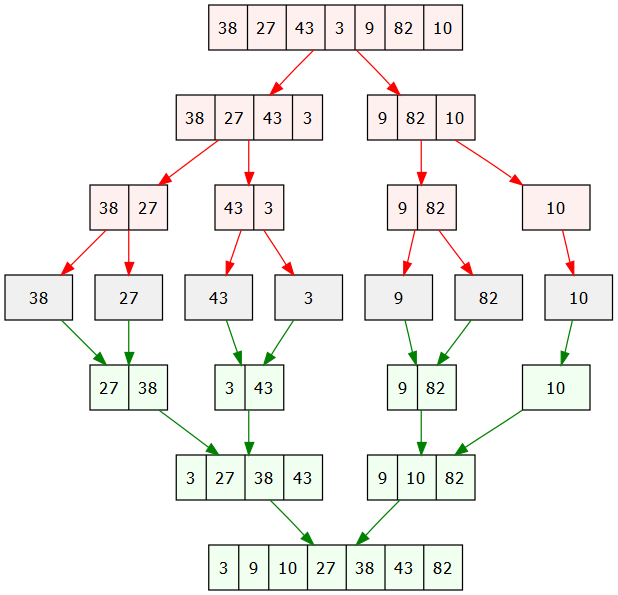
Coding Example
The syntax for setting up a merge sort algorithm in Python would look something like this (we’ll also include an unsorted array):
#Function for merging the arrays
def merge(arr, left, right):
i = j = k = 0
#Copying data into the new arrays
while i < len(left) and j < len (right):
#Checking size of the number in each array
#And storing the smaller one
if left[i] < right[j]:
arr[k] = left[i]
i += 1
else:
arr[k] = right[j]
j += 1
k += 1
#Double-check that the elements were sorted
while i < len(left):
arr[k] = left[i]
i += 1
k += 1
while j < len(right):
arr[k] = right[j]
j += 1
k += 1
#Function for sorting the array
def mergeSort(arr):
if len(arr) > 1:
mid = len(arr)//2
#Storing the elements
#Left and right of the middle
#into their own arrays
L = arr[:mid]
R = arr[mid:]
#Calling this same method on each half
mergeSort(L)
mergeSort(R)
merge (arr, L, R)
#Driver code
arr = [99, 99, 99, 8, 2, 4, 5, 9754, 85, 634, 2]
print("Original Array:")
print(arr)
mergeSort(arr)
print ("Final Sorted Array:")
print (arr)The two operations of merging and sorting are separated into different functions for the sake of clarity. Let’s begin with the “merge” function, which, by its title, will start merging arrays; first off, note that the numbers i, j, and k are the indexes of the left array, right array, and final array respectively. Since the array we’re dealing with is a set of numbers, we compare each number in the left array to a number at the same position in the right array. We then store the smaller element/lesser value of those numbers into the original array and continue down each left and right array until we’ve run out of entries.
For the sorting portion of the algorithm which will create our sub arrays, notice that it first divides the array into two halves. The function then calls itself for each half. By doing this, we end up with an array for each element of the original array. By having a condition at the beginning, we make sure that the “mergeSort” function is only called when there is more than one entry in the array.
If we run this script the console would output the following array from our example array:
Original Array: [99, 99, 99, 8, 2, 4, 5, 9754, 85, 634, 2] Final Sorted Array: [2, 2, 4, 5, 8, 85, 99, 99, 99, 634, 9754]
A merge sort algorithm is a solid solution for many sorting problems. Unlike other sorting algorithms, it is very time efficient (i.e. less time complexity). However, because it creates a large number of arrays, it can be more memory-intensive than other algorithms, so has a bit more space complexity. Thus, if memory is a concern, do consider looking at an alternative sorting algorithm outside of merge processes – of which there are many (such as insertion sort or the quick sort sorting technique).
You might also find it helpful to explore how to implement a recursive algorithm, as this can have implications for how you get your sorted subarrays and ultimate sorted order.
More Resources
Wikipedia goes into more details about efficiency:
Tutorials with more coding examples:
- Merge Sort – KhanAcademy
- Merge Sort – HackerEarth
- Merge Sort – InterviewBit
- Merge Sort In Java – JavaTPoint
Videos that cover merge sort:
- Merge Sort Algorithm – mycodeschool
- Analysis of Merge sort algorithm – mycodeschool
- Merge sort in 3 minutes – Michael Sambol
- Java: MergeSort explained – Joe James
Did you come across any errors in this tutorial? Please let us know by completing this form and we’ll look into it!

FINAL DAYS: Unlock coding courses in Unity, Godot, Unreal, Python and more.






